As with my last post, I'm trying to catch up here in linking to my recent Bloomberg pieces. This is my last one from two weeks ago. Given all the recent discussion of rising inequality, I wanted to point to a really fascinating paper from about 15 years ago that almost no one (in economics, at least) seems to know about. The paper looks at a very general model of how wealth flows around in an economy, and points to the existence of a surprising phase transition or tipping point in how wealth ends up being distributed. It shows that, beyond a certain threshold (see text below), the usual effect of wealth concentration (a small fraction of people owning a significant fraction of all wealth) becomes much worse: wealth "condenses" into the hands of just a few individuals (or, in the model, they might also be firms), not merely into the hands of a small fraction of the population.
Are we approaching such a point? I've mentioned some evidence in the article that we might be. But the important thing, I believe, is that we have good reason to expect that such a threshold really does exist. We are likely getting closer to it, although we may still have a ways to go.
****
We know that inequality is on the rise around the world: The richest 1 percent command almost half the planet’s household wealth, while the poorest half have less than 1 percent. We know a lot less about why this is happening, and where it might lead.
Some argue that technological advancement drives income disproportionately to those with the right knowledge and skills. Others point to the explosive growth in the financial sector. Liberals worry that extreme inequality will tear society apart. Conservatives argue that the wealth of the rich inspires others to succeed.
What if we could shed all our political prejudices and take a more scientific approach, setting up an experimental world where we could test our thinking about what drives inequality? Crazy as the idea might sound, it has actually been done. The results are worth pondering.
Imagine a world like our own, only greatly simplified. Everyone has equal talent and starts out with the same wealth. Each person can gain or lose wealth by interacting and exchanging goods and services with others, or by making investments that earn uncertain returns over time.
More than a decade ago some scientists set up such a world, in a computer, and used it to run simulations examining fundamental aspects of wealth dynamics. They found several surprising things.
First, inequality was unavoidable: A small fraction of individuals (say 20 percent) always came to possess a large fraction (say 80 percent) of the total wealth. This happened because some individuals were luckier than others. By chance alone, some peoples’ investments paid off many times in a row. The more wealth they had, the more they could invest, making bigger future gains even more likely.
For those who worry about the corrosive effects of wealth inequality on social cohesion and democracy, the idea that it follows almost inexorably from the most basic features of modern economies might be unnerving. But there it is. A small fraction owning most of everything is just as natural as having mountains on a planet with plate tectonics.
Suppose we reach into this experimental world and, by adjusting tax incentives or other means, boost the role of financial investment relative to simple economic exchange. What happens then? The distribution of wealth becomes more unequal: The wealth share of the top 20 percent goes from, say, 80 percent to 90 percent.
If you keep boosting the role of finance and investment, something surprising happens. Inequality doesn’t just keep growing in a gradual and continuous way. Rather, the economy crosses an abrupt tipping point. Suddenly, a few individuals end up owning everything.
This would be a profoundly different world. It’s one thing to have much of the wealth belonging to a small fraction of the population -- 1 percent is still about 70 million people. It’s entirely another if a small number of people -- say, five or eight -- hold most of the wealth. With such a chasm between the poor and rich, the idea that a person could go from one group to the other in a lifetime, or even in a number of generations, becomes absurd. The sheer numbers make the probability vanishingly small.
Are we headed toward such a world? Well, data from Bloomberg and the bank Credit Suisse suggest that the planet’s 138 richest people currently command more wealth than the roughly 3.5 billion who make up the poorest half of the population. Of course, nobody can say whether that means we’ve reached a tipping point or are nearing one.
Experimental worlds are useful in that they exploit the power of computation to examine the likely consequences of complex interactions that would otherwise overwhelm our analytical skills. We can get at least a little insight into what might happen, what we ought to expect.
Our experimental world suggests that today’s vast wealth inequality probably isn’t the result of any economic conspiracy, or of vast differences in human skills. It’s more likely the banal outcome of a fairly mechanical process -- one that, unless we find some way to alter its course, could easily carry us into a place where most of us would rather not be.
Showing posts with label models. Show all posts
Showing posts with label models. Show all posts
Friday, February 14, 2014
Wall St shorts economists
I've been remiss in not providing links to my last two Bloomberg pieces. Active web surfers may have run across them, but if not -- below is the full text of this essay from January. It looks at the question -- first raised here by Noah Smith -- of why, if DSGE models are so useful for understanding an economy, i.e. for gaining insights which can be had in no other way, no one on Wall St. actually seems to use them. Good question, I think:
****
In 1986, when the space shuttle Challenger exploded 73 seconds after takeoff, investors immediately dumped the stock of manufacturer Morton Thiokol Inc., which made the O-rings that were eventually blamed for the disaster. With extraordinary wisdom, the global market had quickly rendered a verdict on what happened and why.
Economists often remind us that markets, by pooling information from diverse sources, do a wonderful job of valuing companies, ideas and inventions. So what does the market think about economic theory itself? The answer ought to be rather disconcerting.
Blogger Noah Smith recently did an informal survey to find out if financial firms actually use the “dynamic stochastic general equilibrium” models that encapsulate the dominant thinking about how the economy works. The result? Some do pay a little attention, because they want to predict the actions of central banks that use the models. In their investing, however, very few Wall Street firms find the DSGE models useful.
I heard pretty much the same story in recent meetings with 15 or so leaders of large London investment firms. None thought that the DSGE models offered insight into the workings of the economy.
This should come as no surprise to anyone who has looked closely at the models. Can an economy of hundreds of millions of individuals and tens of thousands of different firms be distilled into just one household and one firm, which rationally optimize their risk-adjusted discounted expected returns over an infinite future? There is no empirical support for the idea. Indeed, research suggests that the models perform very poorly.
Economists may object that the field has moved on, using more sophisticated models that include more players with heterogeneous behaviors. This is a feint. It isn’t true of the vast majority of research.
Why does the profession want so desperately to hang on to the models? I see two possibilities. Maybe they do capture some deep understanding about how the economy works, an “if, then” relationship so hard to grasp that the world’s financial firms with their smart people and vast resources haven’t yet been able to figure out how to profit from it. I suppose that is conceivable.
More likely, economists find the models useful not in explaining reality, but in telling nice stories that fit with established traditions and fulfill the crucial goal of getting their work published in leading academic journals. With mathematical rigor, the models ensure that the stories follow certain cherished rules. Individual behavior, for example, must be the result of optimizing calculation, and all events must eventually converge toward a benign equilibrium in which all markets clear.
A creative economist colleague of mine told me that his papers have often been rejected from leading journals not for being implausible or for conflicting with the data, but with a simple comment: “This is not an equilibrium model.”
Knowledge really is power. I know of at least one financial firm in London that has a team of meteorologists running a bank of supercomputers to gain a small edge over others in identifying emerging weather patterns. Their models help them make good profits in the commodities markets. If economists’ DSGE models offered any insight into how economies work, they would be used in the same way. That they are not speaks volumes.
Markets, of course, aren’t always wise. They do make mistakes. Maybe we’ll find out a few years from now that the macroeconomists really do know better than all the smart people with “skin in the game.” I wouldn’t bet on it.
****
In 1986, when the space shuttle Challenger exploded 73 seconds after takeoff, investors immediately dumped the stock of manufacturer Morton Thiokol Inc., which made the O-rings that were eventually blamed for the disaster. With extraordinary wisdom, the global market had quickly rendered a verdict on what happened and why.
Economists often remind us that markets, by pooling information from diverse sources, do a wonderful job of valuing companies, ideas and inventions. So what does the market think about economic theory itself? The answer ought to be rather disconcerting.
Blogger Noah Smith recently did an informal survey to find out if financial firms actually use the “dynamic stochastic general equilibrium” models that encapsulate the dominant thinking about how the economy works. The result? Some do pay a little attention, because they want to predict the actions of central banks that use the models. In their investing, however, very few Wall Street firms find the DSGE models useful.
I heard pretty much the same story in recent meetings with 15 or so leaders of large London investment firms. None thought that the DSGE models offered insight into the workings of the economy.
This should come as no surprise to anyone who has looked closely at the models. Can an economy of hundreds of millions of individuals and tens of thousands of different firms be distilled into just one household and one firm, which rationally optimize their risk-adjusted discounted expected returns over an infinite future? There is no empirical support for the idea. Indeed, research suggests that the models perform very poorly.
Economists may object that the field has moved on, using more sophisticated models that include more players with heterogeneous behaviors. This is a feint. It isn’t true of the vast majority of research.
Why does the profession want so desperately to hang on to the models? I see two possibilities. Maybe they do capture some deep understanding about how the economy works, an “if, then” relationship so hard to grasp that the world’s financial firms with their smart people and vast resources haven’t yet been able to figure out how to profit from it. I suppose that is conceivable.
More likely, economists find the models useful not in explaining reality, but in telling nice stories that fit with established traditions and fulfill the crucial goal of getting their work published in leading academic journals. With mathematical rigor, the models ensure that the stories follow certain cherished rules. Individual behavior, for example, must be the result of optimizing calculation, and all events must eventually converge toward a benign equilibrium in which all markets clear.
A creative economist colleague of mine told me that his papers have often been rejected from leading journals not for being implausible or for conflicting with the data, but with a simple comment: “This is not an equilibrium model.”
Knowledge really is power. I know of at least one financial firm in London that has a team of meteorologists running a bank of supercomputers to gain a small edge over others in identifying emerging weather patterns. Their models help them make good profits in the commodities markets. If economists’ DSGE models offered any insight into how economies work, they would be used in the same way. That they are not speaks volumes.
Markets, of course, aren’t always wise. They do make mistakes. Maybe we’ll find out a few years from now that the macroeconomists really do know better than all the smart people with “skin in the game.” I wouldn’t bet on it.
Friday, November 15, 2013
This guy has some issues with Rational Expectations
I just happened across this interesting panel discussion from a couple years ago featuring a number of economists involved with the Rational Expectations movement, either as key proponents (Robert Lucas) or critics (Bob Shiller). A fascinating exchange comes late on when they discuss Jack Muth -- ostensibly the inventor of the idea, although others trace it back to an early paper of Herb Simon -- and Muth's later attitude on this assumption. It seems that Muth came to doubt the usefulness of the idea after he looked at the behaviour of some business firms and found that they didn't seem to follow the Rational Expectations paradigm at all. He thought, therefore, that it would make sense to employ some more plausible and realistic ideas about how people form expectations, and he pointed, even in the early 1980s, to the work of Kahneman and Tversky.
I'm just going to quote the extended exchange below, including a comment from Shiller who makes the fairly obvious point that if economics is about human behavior and how it influences economic outcomes, then there clearly ought to be a progressive interchange between psychology and economics, and from Lucas who, amazingly enough, seems to find this idea utterly abhorrent, apparently because it may spoil economics as a pure mathematical playground. That's my reading at least:
Lovell
I wish Jack Muth could be here to answer that question, but obviously he can’t because he died just as Hurricane Wilma was zeroing in on his home on the Florida Keys. But he did send me a letter in 1984. This was a letter in response to an earlier draft of that paper you are referring to. I sent Jack my paper with some trepidation because it was not encouraging to his theory. And much to my surprise, he wrote back. This was in October 1984. And he said, I came up with some conclusions similar to some of yours on the basis of forecasts of business activity compiled by the Bureau of Business Research at Pitt. [Letter Muth to Lovell (2 October 1984)] He had got hold of the data from five business firms, including expectations data, analyzed it, and found that the rational expectations model did not pass the empirical test.
He went on to say, “It is a little surprising that serious alternatives to rational expectations have never really been proposed. My original paper was largely a reaction against very näıve expectations hypotheses juxtaposed with highly rational decision-making behavior and seems to have been rather widely misinterpreted. Two directions seem to be worth exploring: (1) explaining why smoothing rules work and their limitations and (2) incorporating well known cognitive biases into expectations theory (Kahneman and Tversky). It was really incredible that so little has been done along these lines.”
Muth also said that his results showed that expectations were not in accordance with the facts about forecasts of demand and production. He then advanced an alternative to rational expectations. That alternative he called an “errors-in-the-variables” model. That is to say, it allowed the expectation error to be correlated with both the realization and the prediction. Muth found that his errors-in-variables model worked better than rational expectations or Mills’ implicit expectations, but it did not entirely pass the tests. In a shortened version of his paper published in the Eastern Economic Journal he reported,
“The results of the analysis do not support the hypotheses of the naive, exponential, extrapolative, regressive, or rational models. Only the expectations revision model used by Meiselman is consistently supported by the statistical results. . . . These conclusions should be regarded as highly tentative and only suggestive, however, because of the small number of firms studied. [Muth (1985, p. 200)]
Muth thought that we should not only have rational expectations, but if we’re going to have rational behavioral equations, then consistency requires that our model include rational expectations. But he was also interested in the results of people who do behavioral economics, which at that time was a very undeveloped area.
Hoover
Does anyone else want to comment on issue of testing rational expectations against alternatives and if it matters whether rational expectations stands up to empirical tests or whether it is not the sort of thing for which testing would be relevant?
Shiller
What comes to my mind is that rational expectations models have to assume away the problem of regime change, and that makes them hard to apply. It’s the same criticism they make of Kahnemann and Tversky, that the model isn’t clear and crisp about exactly how you should apply it. Well, the same is true for rational expectations models. And there’s a new strand of thought that’s getting impetus lately, that the failure to predict this crisis was a failure to understand regime changes. The title of a recent book by Carmen Reinhart and Ken Rogoff—the title of the book is This Time Is Different—to me invokes this problem of regime change, that people don’t know when there’s a regime change, and they may assume regime changes too often—that’s a behavioral bias [Carmen Reinhart and Kenneth Rogoff (2009)]. I don’t know how we’re going to model that. Reinhart and Rogoff haven’t come forth with any new answers, but that’s what comes to my mind now, at this point in history. And I don’t know whether you can comment on it: how do we handle the regime change problem? If you don’t have data on subprime mortgages then you build a model that doesn’t have subprime mortgages in it. Also, it doesn’t have the shadow banking sector in it either. Omitting key variables because we don’t have the data history on them creates a fundamental problem That’s why many nice concepts don’t find their way into empirical models and are not used more. They remain just a conceptual model.
Hoover
Bob, do you want to . . . or Dale. . . .
Mortensen
More as a theorist, I am sensitive to that problem. That is the issue. If the world were stable, then rational expectations means simply agents learning about their environment and applying what they learned to their decisions. If the environment’s simple, then how else would you structure the model? It’s precisely—if you like, call it “regime change”—what do you do with unanticipated events? More generally—regime changes is only one of them—you were talking about institutional change that was or wasn’t anticipated. As a theorist, I don’t know how to handle that.
Hoover
Bob, did you want to comment on that? You’re looking unhappy, I thought.
Lucas
No. I mean, you can’t read Muth’s paper as some recipe for cranking out true theories about everything under the sun—we don’t have a recipe like that. My paper on expectations and the neutrality of money was an attempt to get a positive theory about what observations we call a Phillips curve. Basically it didn’t work. After several years, trying to push that model in a direction of being more operational, it didn’t seem to explain it. So we had what we call price stickiness, which seems to be central to the way the system works. I thought my model was going to explain price stickiness, and it didn’t. So we’re still working on it; somebody’s working on it. I don’t think we have a satisfactory solution to that problem, but I don’t think that’s a cloud over Muth’s work. If Jack thinks it is, I don’t agree with him. Mike cites some data that Jack couldn’t make sense out of using rational expectations. . . . There’re a lot of bad models out there. I authored my share, and I don’t see how that affects a lot of things we’ve been talking about earlier on about the value of Muth’s contribution.
Young
Just to wrap up the issue of possible alternatives to rational expectations or complements to rational expectations. Does behavioral economics or psychology in general provide a useful and viable alternative to rational expectations, with the emphasis on “useful”?
Shiller
Well, that’s the criticism of behavioral economics, that it doesn’t provide elegant models. If you read Kahnemann and Tversky, they say that preferences have a kink in them, and that kink moves around depending on framing. But framing is hard to pin down. So we don’t have any elegant behavioral economics models. The job isn’t done, and economists have to read widely and think about these issues. I am sorry, I don’t have a good answer. My opinion is that behavioral economics has to be on the reading list. Ultimately, the whole rationality assumption is another thing; it’s interesting to look back on the history of it. Back at the turn of the century—around 1900—when utility-maximizing economic theory was being discovered, it was described as a psychological theory—did you know that, that utility maximization was a psychological theory? There was a philosopher in 1916—I remember reading, in the Quarterly Journal of Economics —who said that the economics profession is getting steadily more psychological. {laughter} And what did he mean? He said that economists are putting people at the center of the economy, and they’re realizing that people have purposes and they have objectives and they have trade-offs. It is not just that I want something, I’ll consider different combinations and I’ll tell you what I like about that. And he’s saying that before this happened, economists weren’t psychological; they believed in such things as gold or venerable institutions, and they didn’t talk about people. Now the whole economics profession is focused on people. And he said that this is a long-term trend in economics. And it is a long-term trend, so the expected utility theory is a psychological theory, and it reflects some important insights about people. In a sense, that’s all we have, behavioral economics; and it’s just that we are continuing to develop and to pursue it. The idea about rational expectations, again, reflects insights about people—that if you show people recurring patterns in the data, they can actually process it—a little bit like an ARIMA model—and they can start using some kind of brain faculties that we do not fully comprehend. They can forecast—it’s an intuitive thing that evolved and it’s in our psychology. So, I don’t think that there’s a conflict between behavioral economics and classical economics. It’s all something that will evolve responding to each other—psychology and economics.
Lucas
I totally disagree.
Mortensen
I think that we’ve come back around the circle—back to Carnegie again. I was a student of Simon and [Richard] March and [James] Cyert—in fact, I was even a research assistant on A Behavioral Theory of the Firm [Cyert and March (1963)]. So we talked about that in those days too. I am much less up on modern behavioral economics. However, I think what you are referring to are those aspects of psychology that illustrate the limits, if you like, of perception and, say, cognitive ability. Well, Simon did talk about that too—he didn’t use those precise words. What I do see on the question of expectations—right down the hall from me—is my colleague Chuck Manksi [Charles Manksi] and a group of people that he’s associated with. They’re trying to deal with expectations of ordinary people. For a lot of what we are talking about in macroeconomics, we’re thinking of decision-makers sure that they have all the appropriate data and have a sophisticated view about that data. You can’t carry that model of the decision-maker over to many household decisions. And what’s coming out of this new empirical research on expectations is precisely that: how do people think about the uncertainties that go into deciding about what their pension plan is going to look like. I think that those are real issues, where behavioral economics, in that sense, can make a very big contribution to what the rest of us do.
Lucas
One thing economics tries to do is to make predictions about the way large groups of people, say, 280 million people are going to respond if you change something in the tax structure, something in the inflation rate, or whatever. Now, human beings are hugely interesting creatures; so neurophysiology is exciting, cognitive psychology is interesting—I’m still into Freudian psychology—there are lots of different ways to look at individual people and lots of aspects of individual people that are going to be subject to scientific study. Kahnemann and Tversky haven’t even gotten to two people; they can’t even tell us anything interesting about how a couple that’s been married for ten years splits or makes decisions about what city to live in—let alone 250 million. This is like saying that we ought to build it up from knowledge of molecules or—no, that won’t do either, because there are a lot of subatomic particles—we’re not going to build up useful economics in the sense of things that help us think about the policy issues that we should be thinking about starting from individuals and, somehow, building it up from there. Behavioral economics should be on the reading list. I agree with Shiller about that. A well-trained economist or a well-educated person should know something about different ways of looking at human beings. If you are going to go back and look at Herb Simon today, go back and read Models of Man. But to think of it as an alternative to what macroeconomics or public finance people are doing or trying to do . . . there’s a lot of stuff that we’d like to improve—it’s not going to come from behavioral economics. . . at least in my lifetime. {laughter}
Hoover
We have a couple of questions to wrap up the session. Let me give you the next to last one: The Great Recession and the recent financial crisis have been widely viewed in both popular and professional commentary as a challenge to rational expectations and to efficient markets. I really just want to get your comments on that strain of the popular debate that’s been active over the last couple years.
Lucas
If you’re asking me did I predict the failure of Lehmann Brothers or any of the other stuff that happened in 2008, the answer is no.
Hoover
No, I’m not asking you that. I’m asking you whether you accept any of the blame. {laughter} The serious point here is that, if you read the newspapers and political commentary and even if you read commentary among economists, there’s been a lot of talk about whether rational expectations and the efficient-markets hypotheses is where we should locate the analytical problems that made us blind. All I’m asking is what do you think of that?
Lucas
Is that what you get out of Rogoff and Reinhart? You know, people had no trouble having financial meltdowns in their economies before all this stuff we’ve been talking about came on board. We didn’t help, though; there’s no question about that. We may have focused attention on the wrong things; I don’t know.
Shiller
Well, I’ve written several books on that. {laughter} My latest, with George Akerlof, is called Animal Spirits [2009]. And we presented an idea that Bob Lucas probably won’t like. It was something about the Keynesian concept. Another name that’s not been mentioned is John Maynard Keynes. I suspect that he’s not popular with everyone on this panel. Animal Spirits is based on Keynes. He said that animal spirits is a major driver of the economy. To understand Keynes, you have to go back to his 1921 book, Treatise on Probability [Keynes (1921)]. He said—he’s really into almost this regime-change thing that we brought up before—that people don’t have probabilities, except in very narrow, special circumstances. You can think of a coin-toss experiment, and then you know what the probabilities are. But in macroeconomics, it’s always fuzzy. What Keynes said in The General Theory [1936] is that, if people are really thoroughly rational, they would be paralyzed into inaction, because they just don’t know. They don’t know the kind of things that you would need to put into a decision-theory framework. But they do act, and so there is something that drives people—it’s animal spirits. You’re lying in bed in the morning and you could be thinking, “I don’t know what’s going to happen to me today; I could get hit by a truck; I just will stay in bed all day.” But you don’t. So animal spirits is the core of—maybe I’m telling this too bluntly—but it fluctuates. Sometimes it is represented as confidence, but it is not necessarily confidence. It is trust in each other, our sense of whether other people think that we’re moving ahead or . . . something like that. I believe that’s part of what drives the economy. It’s in our book, and it’s not very well modeled yet. But Keynes never wrote his theory down as a model either. He couldn’t do it; he wasn’t ready. These are ideas that, even to this day, are fuzzy. But they have a hold on people. I’m sure that Ben Bernanke and Austin Goolsbee are influenced by John Maynard Keynes, who was absolutely not a rational-expectations theorist. And that’s another strand of thought. In my mind, the strands are not resolved, and they are both important ways of looking at the world.
Wednesday, November 13, 2013
Beating the dead horse of rational expectations...
The above award should be given to University of Oxford economist Simon Wren-Lewis for concocting yet another defense of the indefensible idea of Rational Expectations (RE). Gotta admire his determination. I've written about this idea many times (here and here, for example), and I thought it had died a death, but that was obviously not true. I'm not going to say too much except to note that the strategy of the Wren-Lewis argument is essentially to ask "what are the alternatives to Rational Expectations?," then to mention just one possible alternative that he calls "naive adaptive expectations," and then to go on to criticize this silly alternative as being unrealistic, which it indeed is. But that's no defense of RE.
He doesn't ever address the question of why economists don't use more realistic ways to model how people form their expectations, for example by looking to psychology and experimental studies of how people learn (especially through social interactions and copying behavior). The only defense he offers on that score is to say they don't want too many details because they seek a "simple" way to model expectations so they can solve their favorite macroeconomic models. That fact that this renders such models possibly quite useless and misleading as guides to the real world doesn't seem to give him (or others) pause.
Lars Syll was a target in the Wren-Lewis post and has a nice rejoinder here. In comments, others raised concerns about why Lars didn't mentioned specific alternatives to RE. I added a comment there, which I'll reproduce here:
It seems to me that there are clear alternatives to rational expectations and I'm not sure why economists seem loath to use then. Simon Wren-Lewis gives one alternative as naive "adaptive expectations", but this seems like a straw man. Here people seem to believe more or less that trends will continue. That is truly naive. Expectations are important and the psychological literature on learning suggests that people form them in many ways, with heuristic theories and rules of thumb, and then adjust their use of these heuristics through experience. This is the kind of adaptive expectations that ought to be used in macro models.One day soon I hope this subject really will be a dead horse.
From what I have read, however, the vast "learning literature" in macroeconomics that defenders of RE often refer to really doesn't go very far in exploring learning. A review I read as recently as 2009 used learning algorithms which ASSUMED that people already know the right model of the economy and only need to learn the values of some parameters. I suspect this is done on purpose so that the learning process converges to RE -- and an apparent defense of RE is therefore achieved. But this is only a trick. Use more realistic learning behavior to model expectations and you find little convergence at all -- just ongoing learning as the economy itself keeps doing new things in ways the participants never quite manage to predict.
As Simon Wren-Lewis himself notes, " it is worth noting that a key organising device for much of the learning literature is the extent to which learning converges towards rational expectations." So again, it seems as if the purpose of the model is to see how we can get the conclusion we want, not to explore the kinds of things we might actually expect to see in the world. This is what makes people angry and I think rightfully about the RE idea. I suspect that REAL reason for this is that, if one uses more plausible learning behavior (not the silly naive kind of adaptive expectations), you find that your economy isn't guaranteed to settle down to any kind of equilibrium, and you can't say anything honestly about the welfare of any outcomes, and so most of what has been developed in economics turns out to be pretty useless. Most economists find that too much to stomach.
Wednesday, April 10, 2013
Model abuse... stop it now!
I think we would benefit from better and more realistic models of systems in economics and finance, better models for imagining and assessing risks, and so on. But it is true that having a better model is one thing, using it another entirely. A commenter on my recent Bloomberg piece on agent-based models pointed me to this post, which looks at some examples of how risk models in finance (ones this author had helped develop) were repeatedly abused and distorted to suit the needs of higher ups:
For a person like myself, who gets paid to “fix the model,” it’s tempting to do just that, to assume the role of the hero who is going to set everything right with a few brilliant ideas and some excellent training data.
Unfortunately, reality is staring me in the face, and it’s telling me that we don’t need more complicated models.
If I go to the trouble of fixing up a model, say by adding counterparty risk considerations, then I’m implicitly assuming the problem with the existing models is that they’re being used honestly but aren’t mathematically up to the task.
But this is far from the case – most of the really enormous failures of models are explained by people lying. Before I give three examples of “big models failing because someone is lying” phenomenon, let me add one more important thing.
Namely, if we replace okay models with more complicated models, as many people are suggesting we do, without first addressing the lying problem, it will only allow people to lie even more. This is because the complexity of a model itself is an obstacle to understanding its results, and more complex models allow more manipulation.
Sunday, April 7, 2013
Mortgage dynamics
My latest Bloomberg column should appear sometime Sunday night 7 April. I've written about some fascinating work that explores the origins of the housing bubble and the financial crisis by using lots of data on the buying/selling behaviour of more than 2 million people over the period in question. It essentially reconstructs the crisis in silico and tests which factors had the most influence as causes of the bubble, i.e. leverage, interest rates and so on.
I think this is a hugely promising way of trying to answer such questions, and I wanted to point to one interesting angle in the history of this work: it came out of efforts on Wall St. to build better models of mortgage prepayments, using any technique that would work practically. The answer was detailed modelling of the actual actions of millions of individuals, backed up by lots of good data.
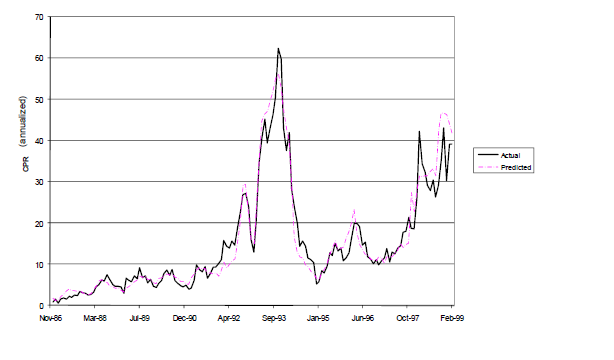
First, take a look at the figure below:
This figure shows the actual (solid line) rate of repayment of a pool of mortgages that were originally issued in 1986. It also shows the predictions (dashed line) for this rate made by an agent-based model of mortgage repayments developed by John Geanakoplos working for two different Wall St. firms. There are two things to notice. First, obviously, the model works very well over the entire period up to 1999. The second, not obvious, is that the model works well even over a period for which it was not designed, by the data, to fit. The sample of data used to build the model went from 1986 through early 1996. The model continues to work well even out of sample over the final three years of this period, roughly 30% beyond the period of fitting. (The model did not work in subsequent years and had to be adjusted due to a major changes in the market itself, after 2000, especially new possibilities to refinance and take cash out of mortgages that were not there before.).
How was this model built? Almost all mortgages give the borrower the right in any month to repay the mortgage in its entirely. Traditionally, models aiming to predict how many would do so worked by trying to guess or develop some function to describe the aggregate behavior of all the mortgage owners, reflecting ideas about individual behavior in some crude way in the aggregate. As Geanakoplos et al. put it:
Models of this kind also capture in a more natural way, with no extra work, things that have to be put in by hand when working only at the aggregate level. In this mortgage example, this is true of the "burnout" -- the gradual lessening of prepayment rates over time (other things being equal):
This is how it was possible, going back up to the figure above, to make accurate predictions of prepayment rates three years out of sample. In a sense, the lesson is that you do better if you really try to make contact with reality, modelling as many realistic details as you have access to. Mathematics alone won't perform miracles, but mathematics based on realistic dynamical factors, however crudely captured, can do some impressive things.
I suggest reading the original, fairly short paper, which was eventually published in the American Economic Review. That alone speaks to at least grudging respect on the part of the larger economics community to the promise of agent based modelling. The paper takes this work on mortgage prepayments as a starting point and an inspiration, and tries to model the housing market in the Washington DC area in a similar way through the period of the housing bubble.
I think this is a hugely promising way of trying to answer such questions, and I wanted to point to one interesting angle in the history of this work: it came out of efforts on Wall St. to build better models of mortgage prepayments, using any technique that would work practically. The answer was detailed modelling of the actual actions of millions of individuals, backed up by lots of good data.
First, take a look at the figure below:
This figure shows the actual (solid line) rate of repayment of a pool of mortgages that were originally issued in 1986. It also shows the predictions (dashed line) for this rate made by an agent-based model of mortgage repayments developed by John Geanakoplos working for two different Wall St. firms. There are two things to notice. First, obviously, the model works very well over the entire period up to 1999. The second, not obvious, is that the model works well even over a period for which it was not designed, by the data, to fit. The sample of data used to build the model went from 1986 through early 1996. The model continues to work well even out of sample over the final three years of this period, roughly 30% beyond the period of fitting. (The model did not work in subsequent years and had to be adjusted due to a major changes in the market itself, after 2000, especially new possibilities to refinance and take cash out of mortgages that were not there before.).
How was this model built? Almost all mortgages give the borrower the right in any month to repay the mortgage in its entirely. Traditionally, models aiming to predict how many would do so worked by trying to guess or develop some function to describe the aggregate behavior of all the mortgage owners, reflecting ideas about individual behavior in some crude way in the aggregate. As Geanakoplos et al. put it:
The conventional model essentially reduced to estimating an equation with an assumed functional form for prepayment rate... Prepay(t) = F(age(t), seasonality(t), old rate – new rate(t), burnout(t), parameters), where old rate – new rate is meant to capture the benefit to refinancing at a given time t, and burnout is the summation of this incentive over past periods. Mortgage pools with large burnout tended to prepay more slowly, presumably because the most alert homeowners prepay first. ...There is of course nothing wrong with this. It's an attempt to do something practically useful with the data then available (which wasn't generally detailed at the level of individual loans). The contrasting approach, seeks instead to start from the characteristics of individual homeowners and to model their behavior, as a population, as it evolves through time:
Note that the conventional prepayment model uses exogenously specified functional forms to describe aggregate behavior directly, even when the motivation for the functional forms, like burnout, is explicitly based on heterogeneous individuals.
the new prepayment model... starts from the individual homeowner and in principle follows every single individual mortgage. It produces aggregate prepayment forecasts by simply adding up over all the individual agents. Each homeowner is assumed to be subject to a cost c of prepaying, which include some quantifiable costs such as closing costs, as well as less tangible costs like time, inconvenience, and psychological costs. Each homeowner is also subject to an alertness parameter a, which represents the probability the agent is paying attention each month. The agent is assumed aware of his cost and alertness, and subject to those limitations chooses his prepayment optimally to minimize the expected present value of his mortgage payments, given the expectations that are implied by the derivatives market about future interest rates.By way of analogy, this is essentially modelling the prepayment behavior of a population of homeowners as an ecologist might model, say, the biomass consumption of some population of insects. The idea would be to follow the density of insects as a function of their size, age and other features that influence how and when and how much they tend to consume. The more you model such features explicitly as a distribution of influential factors, the more likely your model will take on aspects of the real population, and the more likely it will be to make predictions about the future, because it has captured real aspects of the causal factors in the past.
Agent heterogeneity is a fact of nature. It shows up in the model as a distribution of costs and alertness, and turnover rates. Each agent is characterized by an ordered pair (c,a) of cost and alertness, and also a turnover rate t denoting the probability of selling the house. The distribution of these characteristics throughout the population is inferred by fitting the model to past prepayments. The effects of observable borrower characteristics can be incorporated in the model (when they become available) by allowing them to modify the cost, alertness, and turnover.
Models of this kind also capture in a more natural way, with no extra work, things that have to be put in by hand when working only at the aggregate level. In this mortgage example, this is true of the "burnout" -- the gradual lessening of prepayment rates over time (other things being equal):
... burnout is a natural consequence of the agent-based approach; there is no need to add it in afterwards. The agents with low costs and high alertness prepay faster, leaving the remaining pool with slower homeowners, automatically causing burnout. The same heterogeneity that explains why only part of the pool prepays in any month also explains why the rate of prepayment burns out over time.One other thing worth noting is that those developing this model found that to fit the data well they had to include an effect of "contagion", i.e. the spread of behavior directly from one person to another. When prepayment rates go up, it appears they do so not solely because people have independently made optimal decisions to prepay. Fitting the data well demands an assumption that some people become aware of the benefit of prepaying because they have seen or heard about others who have done so.
This is how it was possible, going back up to the figure above, to make accurate predictions of prepayment rates three years out of sample. In a sense, the lesson is that you do better if you really try to make contact with reality, modelling as many realistic details as you have access to. Mathematics alone won't perform miracles, but mathematics based on realistic dynamical factors, however crudely captured, can do some impressive things.
I suggest reading the original, fairly short paper, which was eventually published in the American Economic Review. That alone speaks to at least grudging respect on the part of the larger economics community to the promise of agent based modelling. The paper takes this work on mortgage prepayments as a starting point and an inspiration, and tries to model the housing market in the Washington DC area in a similar way through the period of the housing bubble.
Labels:
agent based,
agents,
bubbles,
housing,
models,
prediction
Monday, February 13, 2012
Approaching the singularity -- in global finance
In a new paper on trends in high-frequency trading, Neil Johnson and colleagues note that:
We may be getting close. If Johnson and his colleagues are correct, the markets are already showing signs of having already made a transition into a machine-dominated phase in which humans have little control.
Most readers here will probably know about futurist Ray Kurzweil's prediction of the approaching "singularity" -- the idea that as our technology becomes increasingly intelligent it will at some point create self-sustaining positive feedback loops that drive explosively faster science and development leading to a kind of super-intelligence residing in machines. Humans will be out of the loop and left behind. Given that so much of the future vision of computing now centers on bio-inspired computing -- computers that operate more along the lines of living organisms, being able do things like self-repair and adaptation, true reproduction, etc, -- it's easy to imagine this super-intelligence again ultimately being strongly biological in form, while also exploiting technologies that earlier evolution was unable to harness (superconductivity, quantum computing, etc.). In that case -- again, if you believe this conjecture has some merit -- it could turn out ironically that all of our computing technology will act as a kind of mid-wife aiding a transition from Homo sapiens to some future non-human but super-intelligent species.
But forget that. Think singularity, but in the smaller world of the markets. Johnson and his colleagues ask the question of whether today's high-frequency markets are moving toward a boundary of speed where human intervention and control is effectively impossible:
In the period from 2006-2011, they found (looking at many stocks on multiple exchanges) that there were about 18,500 specific episodes in which markets, in less than 1.5 seconds, either 1. ticked down at least 10 times in a row, dropping by more than 0.8% or 2. ticked up at least 10 times in a row, rising by more than 0.8%. The figure below shows two typical events, a crash and a spike (upward), both lasting only 25 ms.

Apparently, these very brief and momentary downward crashes or upward spikes -- the authors refer to them as "fractures" or "Black Swan events" -- are about equally likely. And they become more likely as one goes to shorter time intervals:
Ok. Now for the punchline -- an effort to understand how this transition might happen. In my last blog post I wrote about the Minority Game -- a simple model of a market in which adaptive agents attempt to profit by using a variety of different strategies. It reproduces the realistic statistics of real markets, despite its simplicity. I expect that some people may wonder if this model can really be useful in exploring real markets. If so, this new work by Johnson and colleagues offers a powerful example of how valuable the minority game can be in action.
Their hypothesis is that the observed transition in market dynamics below one second reflects "a new fundamental transition from a mixed phase of humans and machines, in which humans have time to assess information and act, to an ultrafast all-machine phase in which machines dictate price changes." They explore this in a model that...
Johnson and colleagues suggests that the transition between these regimes is just what shows up in the statistics around the one second threshold. They first argue that the regime for large α (many strategies per agent) should be associated with the trading regime above one second, where both people and machines take part. Why? As they suggest,
In contrast, they suggest that the sub one second regime should be associated the the α < 1 phase of the minority game:
The paper as a whole takes a bit of time to get your head around, but it is, I think, a beautiful example of how a simple model that explores some of the rich dynamics of how strategies interact in a market can give rise to some deep insights. The analysis suggests, first, that the high frequency markets have moved past "the singularity," their dynamics having become fundamentally different -- uncoupled from the control, or at least strong influence, of human trading. It also suggests, second, that the change in dynamics derives directly from the crowding of strategies that operate on very short timescales, this crowding caused by the need for relative simplicity in these strategies.
This kind of analysis really should have some bearing on the consideration of potential new regulations on HFT. But that's another big topic. Quite aside from practical matters, the paper shows how valuable perspectives and toy models like the minority game might be.
... a new dedicated transatlantic cable is being built just to shave 5 milliseconds off transatlantic communication times between US and UK traders, while a new purpose-built chip iX-eCute is being launched which prepares trades in 740 nanoseconds ...This just illustrates the technological arms race underway as firms try to out-compete each other to gain an edge through speed. None of the players in this market worries too much about what this arms race might mean for the longer term systemic stability of market; it's just race ahead and hope for the best. I've written before (here and here) about some analyses (notably from Andrew Haldane of the Bank of England) suggesting that this race is generally increasing market volatility and will likely lead to disaster in one form or another.
We may be getting close. If Johnson and his colleagues are correct, the markets are already showing signs of having already made a transition into a machine-dominated phase in which humans have little control.
Most readers here will probably know about futurist Ray Kurzweil's prediction of the approaching "singularity" -- the idea that as our technology becomes increasingly intelligent it will at some point create self-sustaining positive feedback loops that drive explosively faster science and development leading to a kind of super-intelligence residing in machines. Humans will be out of the loop and left behind. Given that so much of the future vision of computing now centers on bio-inspired computing -- computers that operate more along the lines of living organisms, being able do things like self-repair and adaptation, true reproduction, etc, -- it's easy to imagine this super-intelligence again ultimately being strongly biological in form, while also exploiting technologies that earlier evolution was unable to harness (superconductivity, quantum computing, etc.). In that case -- again, if you believe this conjecture has some merit -- it could turn out ironically that all of our computing technology will act as a kind of mid-wife aiding a transition from Homo sapiens to some future non-human but super-intelligent species.
But forget that. Think singularity, but in the smaller world of the markets. Johnson and his colleagues ask the question of whether today's high-frequency markets are moving toward a boundary of speed where human intervention and control is effectively impossible:
The downside of society’s continuing drive toward larger, faster, and more interconnected socio-technical systems such as global financial markets, is that future catastrophes may be less easy to forsee and manage -- as witnessed by the recent emergence of financial flash-crashes. In traditional human-machine systems, real-time human intervention may be possible if the undesired changes occur within typical human reaction times. However,... in many areas of human activity, the quickest that someone can notice such a cue and physically react, is approximately 1000 milliseconds (1 second)Obviously, most trading now happens much faster than this. Is this worrying? With the authors, let's look at the data.
In the period from 2006-2011, they found (looking at many stocks on multiple exchanges) that there were about 18,500 specific episodes in which markets, in less than 1.5 seconds, either 1. ticked down at least 10 times in a row, dropping by more than 0.8% or 2. ticked up at least 10 times in a row, rising by more than 0.8%. The figure below shows two typical events, a crash and a spike (upward), both lasting only 25 ms.
Apparently, these very brief and momentary downward crashes or upward spikes -- the authors refer to them as "fractures" or "Black Swan events" -- are about equally likely. And they become more likely as one goes to shorter time intervals:
... our data set shows a far greater tendency for these financial fractures to occur, within a given duration time-window, as we move to smaller timescales, e.g. 100-200ms has approximately ten times more than 900-1000ms.But they also find something much more significant. They studied the distribution of these events by size, and considered if this distribution changes when looking at events taking place on different timescales. The data suggests that it does. For times above about 0.8 seconds or so, the distribution closely fits a power law, in agreement with countless other studies of market returns on times of one second or longer. For times shorter than about 0.8 seconds, the distribution begins to depart from the power law form. (It's NOT that it becomes more Gaussian, but it does become something else that is not a power law.) The conclusion is that something significant happens in the market when we reach times going below 1 second -- roughly the timescale of human action.
Ok. Now for the punchline -- an effort to understand how this transition might happen. In my last blog post I wrote about the Minority Game -- a simple model of a market in which adaptive agents attempt to profit by using a variety of different strategies. It reproduces the realistic statistics of real markets, despite its simplicity. I expect that some people may wonder if this model can really be useful in exploring real markets. If so, this new work by Johnson and colleagues offers a powerful example of how valuable the minority game can be in action.
Their hypothesis is that the observed transition in market dynamics below one second reflects "a new fundamental transition from a mixed phase of humans and machines, in which humans have time to assess information and act, to an ultrafast all-machine phase in which machines dictate price changes." They explore this in a model that...
...considers an ecology of N heterogenous agents (machines and/or humans) who repeatedly compete to win in a competition for limited resources. Each agent possesses s > 1 strategies. An agent only participates if it has a strategy that has performed sufficiently well in the recent past. It uses its best strategy at a given timestep. The agents sit watching a common source of information, e.g. recent price movements encoded as a bit-string of length M, and act on potentially profitable patterns they observe.This is just the minority game as I described it a few days ago. One of the truly significant lessons emerging from its study is that we should expect markets to have two fundamentally distinct phases of dynamics depending on the parameter α=P/N, where P is the number of different past histories the agents can perceive, and N is the number of agents in the game. [P=2M if the agents use bit strings of length M in forming their strategies]. If α is small, then there are lots of players relative to the number of different market histories they can perceive. If α is big, then there are many different possible histories relative to only a few people. These two extremes lead to very different market behaviour.
Johnson and colleagues suggests that the transition between these regimes is just what shows up in the statistics around the one second threshold. They first argue that the regime for large α (many strategies per agent) should be associated with the trading regime above one second, where both people and machines take part. Why? As they suggest,
We associate this regime (see Fig. 3) with a market in which both humans and machines are dictating prices, and hence timescales above the transition (>1s), for these reasons: The presence of humans actively trading -- and hence their ‘free will’ together with the myriad ways in which they can manually override algorithms -- means that the effective number (i.e. α > 1). Moreover α > 1 implies m is large, hence there are more pieces of information available which suggests longer timescales... in this α > 1 regime, the average number of agents per strategy is less than 1, hence any crowding effects due to agents coincidentally using the same strategy will be small. This lack of crowding leads our model to predict that any large price movements arising for α > 1 will be rare and take place over a longer duration – exactly as observed in our data for timescales above 1000ms. Indeed, our model’s price output (e.g. Fig. 3, right-hand panel) reproduces the stylized facts associated with financial markets over longer timescales, including a power-law distribution.What they're getting at here is that crowding in the space of strategies, by creating strong correlations in the strategies of different agents, should tend to make large market movements more likely. After all, if lots of agents come to use the very same strategy, they will all trade the same way at the same time. In this regime above one second, with humans and machine, they suggests there shouldn't be much crowding; the dynamics here do give a power law distribution of movements, but it is what is found in all markets in this regime.
In contrast, they suggest that the sub one second regime should be associated the the α < 1 phase of the minority game:
Our association of the α < 1 regime with an all-machine phase is consistent with the fact that trading algorithms in the sub-second regime need to be executable extremely quickly and hence be relatively simple, without calling on much memory concerning past information: α < 1 regime with an all-machine phase is consistent with the fact that trading algorithms in the sub-second regime need to be executable extremely quickly and hence be relatively simple, without calling on much memory concerning past information: Hence M will be small, so the total number of strategies will be small and therefore... α < 1. Our model also predicts that the size distribution for the black swans in this ultrafast regime (α < 1) should not have a power law since changes of all sizes do not appear – this is again consistent with the results in Fig. 2.And...
Our model undergoes a transition around α = 1 to a regime characterized by significant strategy crowding and hence large fluctuations. The price output for α < 1 (Fig. 3, left-hand panel) shows frequent abrupt changes due to agents moving as unintentional groups into particular strategies. Our model therefore predicts a rapidly increasing number of ultrafast black swan events as we move to smaller α and hence smaller subsecond timescales – as observed in our data.The authors go on to quantify this transition in a little more detail. In particular, they calculate in the simple minority game model the standard deviation of the price fluctuations. In the regime α < 1 this turns out to be roughly proportional to the number N of agents in the market. In contrast, it goes in proportion only to the square root of N in the α > 1 regime. Hence, the model predicts a sharp increase in the size of market fluctuations when entering the machine dominated phase below one second.
The paper as a whole takes a bit of time to get your head around, but it is, I think, a beautiful example of how a simple model that explores some of the rich dynamics of how strategies interact in a market can give rise to some deep insights. The analysis suggests, first, that the high frequency markets have moved past "the singularity," their dynamics having become fundamentally different -- uncoupled from the control, or at least strong influence, of human trading. It also suggests, second, that the change in dynamics derives directly from the crowding of strategies that operate on very short timescales, this crowding caused by the need for relative simplicity in these strategies.
This kind of analysis really should have some bearing on the consideration of potential new regulations on HFT. But that's another big topic. Quite aside from practical matters, the paper shows how valuable perspectives and toy models like the minority game might be.
Subscribe to:
Posts (Atom)